We all know the algorithm for calculating Fibonacci numbers:
int fib( int n ) {
if ( n < 2 ) return n;
else
return fib(n-1) + fib(n-2);
}
This algorithm is commonly used as an example of the elegance
of recursion as a programming technique.
However, when we examine its time complexity, we find it's
far from elegant!
Analysis
If tn is the time required to calculate fn, where fn is the nth Fibonacci number. Then, by examining the function above, it's clear thatTherefore
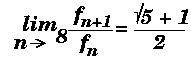
An Iterative Solution
However, this simple alternative:int fib( int n ) {
int k, f1, f2;
if ( n < 2 ) return n;
else {
f1 = f2 = 1;
for(k=2;k<n;k++) {
f = f1 + f2;
f2 = f1;
f1 = f;
}
return f;
}
runs in O(n) time.
This algorithm solves the problem of calculating f0 and f1 first, calculates f2 from these, then f3 from f2 and f1, and so on. Thus, instead of dividing the large problem into two (or more) smaller problems and solving those problems (as we did in the divide and conquer approach), we start with the simplest possible problems. We solve them (usually trivially) and save these results. These results are then used to solve slightly larger problems which are, in turn, saved and used to solve larger problems again.
Free Lunch?
As we know, there's never one! Dynamic problems obtain their efficiency by solving and storing the answers to small problems. Thus they usually trade space for increased speed. In the Fibonacci case, the extra space is insignificant - the two variables f1 and f2, but in some more complex dynamic algorithms, we'll see that the space used is significant.